Suma De Fracciones Para Niños De Tercero De Primaria aborda el concepto de fracciones y su suma de una manera sencilla y fácil de entender para los jóvenes estudiantes. Esta guía paso a paso proporciona una base sólida para que los niños dominen esta habilidad matemática esencial.
A través de ejemplos claros y ejercicios prácticos, este artículo guiará a los niños a través de los procedimientos para sumar fracciones con el mismo y diferente denominador, cubriendo también casos especiales como fracciones con numerador o denominador cero y fracciones mixtas.
Concepto de suma de fracciones
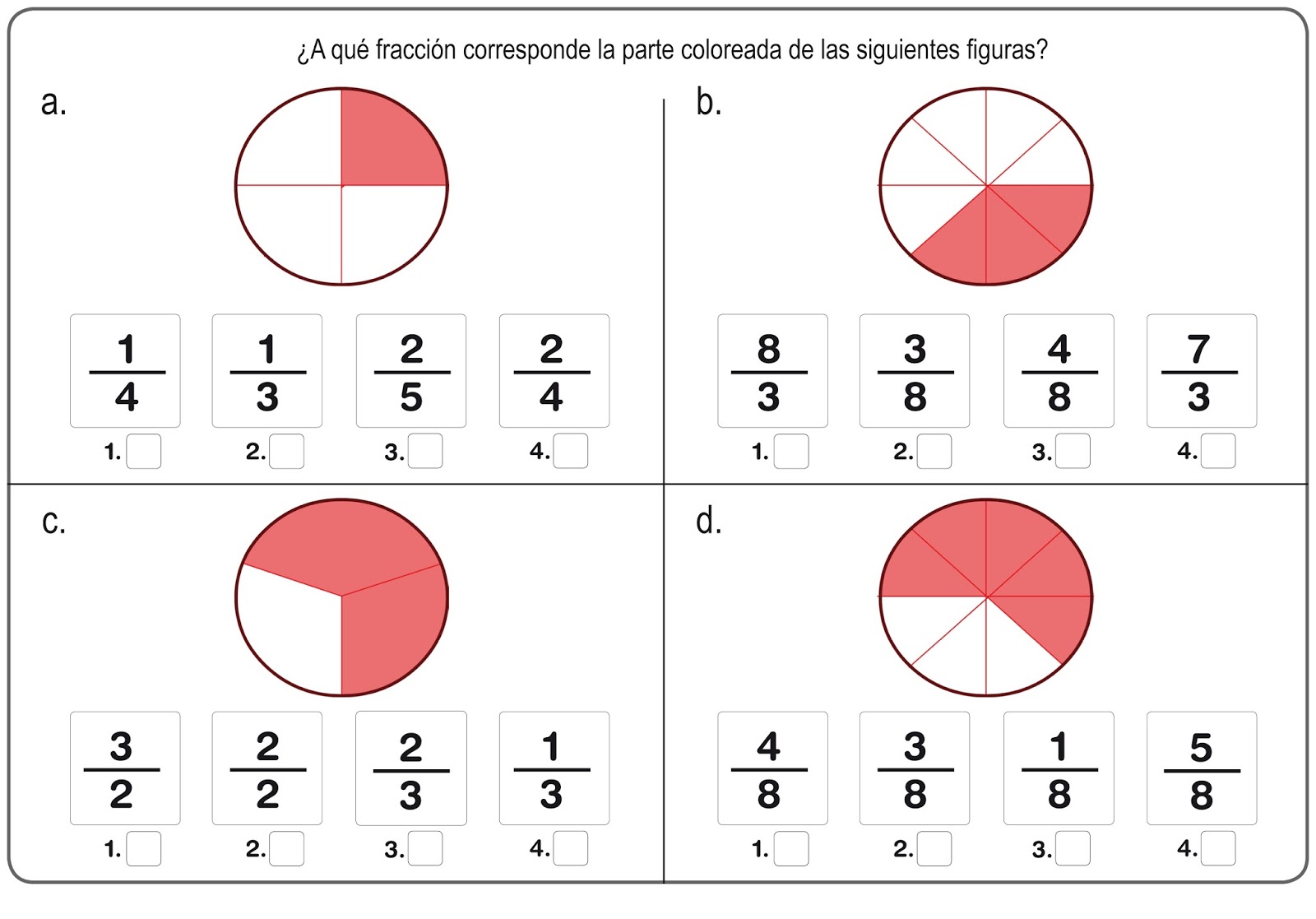
Una fracción es una forma de representar una parte de un todo. Se escribe como dos números separados por una barra: el numerador (arriba) y el denominador (abajo). El numerador indica cuántas partes se toman, mientras que el denominador indica en cuántas partes se divide el todo.La
suma de fracciones es la operación de combinar dos o más fracciones para obtener una nueva fracción que represente el total de las partes tomadas. Para sumar fracciones, los denominadores deben ser iguales. Si no lo son, primero hay que convertirlas a fracciones equivalentes con el mismo denominador.Ejemplos
de suma de fracciones:* 1/2 + 1/2 = 2/2 = 1
- 1/4 + 1/4 = 2/4 = 1/2
- 1/3 + 1/6 = 2/6 + 1/6 = 3/6 = 1/2
Procedimiento para sumar fracciones con igual denominador
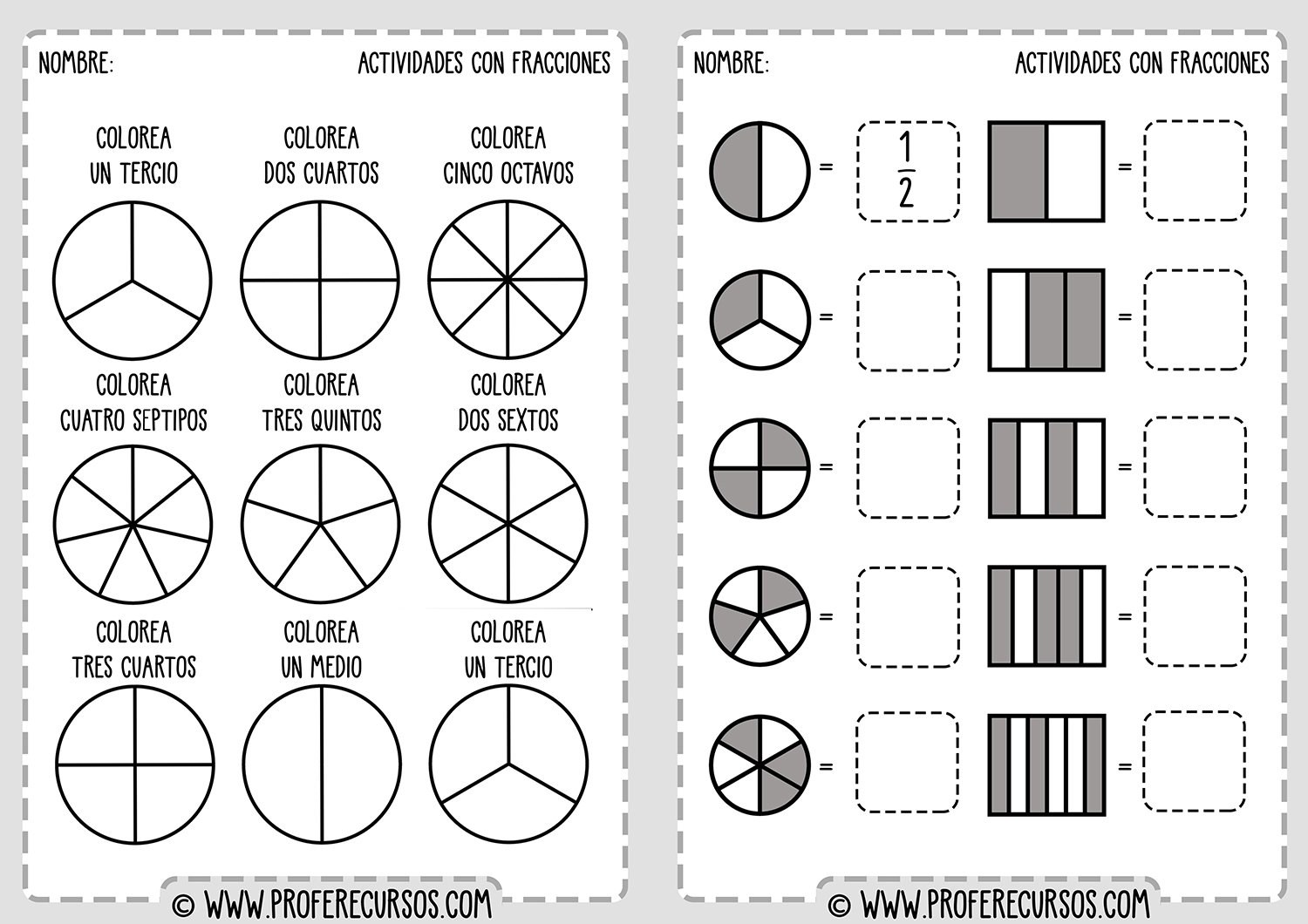
Sumar fracciones con igual denominador es sencillo. Solo hay que sumar los numeradores y mantener el mismo denominador.
Pasos:
- Sumar los numeradores de las fracciones.
- Mantener el mismo denominador.
Ejemplo:
| Numerador | Denominador | Suma |
|---|---|---|
| 1 | 3 | 2 |
| 1 | 3 |
1/3 + 1/3 = (1 + 1)/3 = 2/3
Procedimiento para sumar fracciones con diferente denominador

Para sumar fracciones con diferente denominador, debemos encontrar un denominador común para ambas fracciones.
El denominador común más pequeño (mcm) es el múltiplo común más pequeño de los denominadores de las fracciones.
Pasos para encontrar el mcm:
- Encuentra los factores primos de cada denominador.
- Multiplica los factores primos comunes y no comunes con el mayor exponente de cada factor.
Pasos para sumar fracciones con diferente denominador:
- Encuentra el mcm de los denominadores.
- Multiplica el numerador y el denominador de cada fracción por un factor que haga que su denominador sea el mcm.
- Suma los numeradores de las fracciones y mantén el denominador común.
- Simplifica la fracción resultante, si es posible.
Ejemplo:, Suma De Fracciones Para Niños De Tercero De Primaria
Suma las fracciones 1/2 y 1/3:
- El mcm de 2 y 3 es 6.
- Multiplica 1/2 por 3/3 y 1/3 por 2/2:
- Suma las fracciones:
1/2 = 3/6
1/3 = 2/6
3/6 + 2/6 = 5/6
Por lo tanto, 1/2 + 1/3 = 5/6.
Casos especiales en la suma de fracciones: Suma De Fracciones Para Niños De Tercero De Primaria
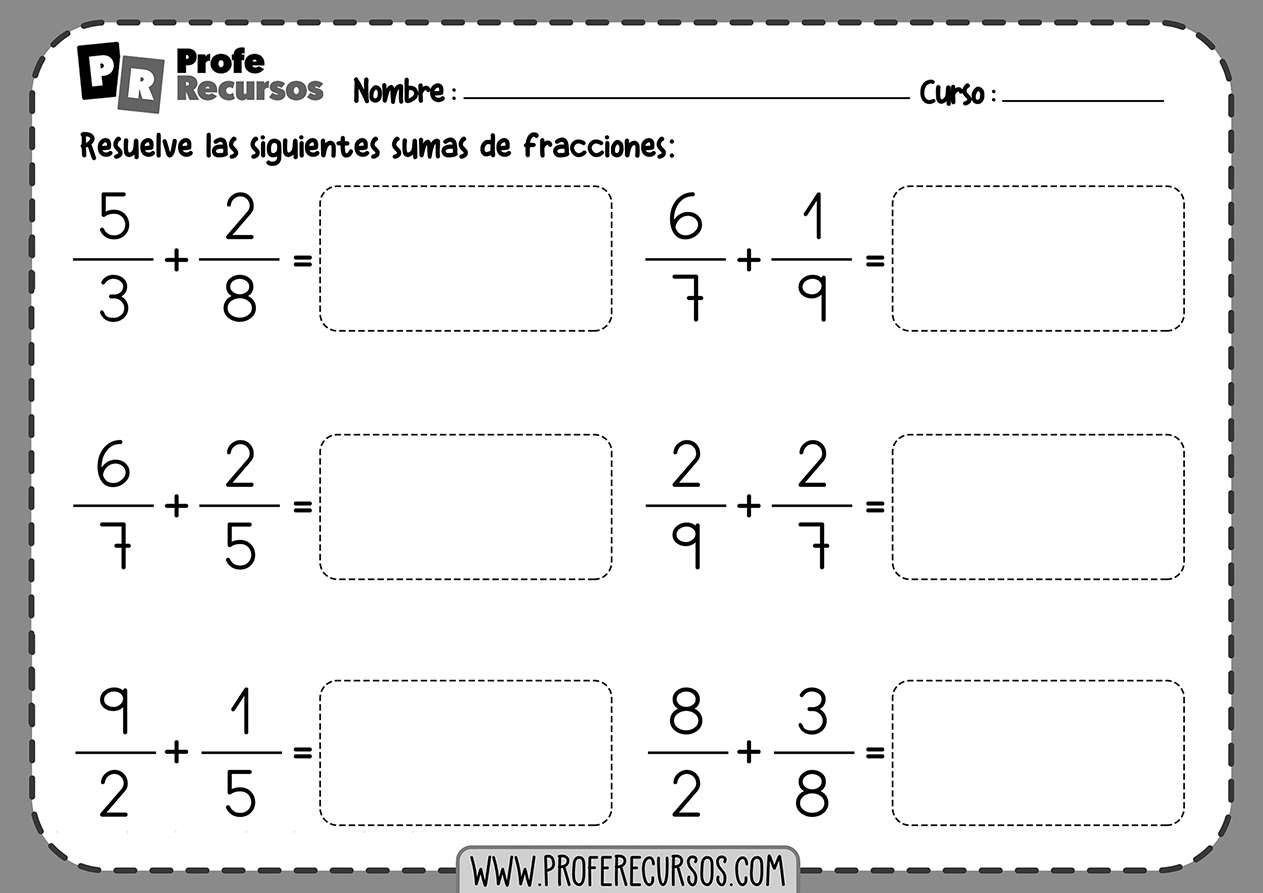
En la suma de fracciones, pueden surgir algunos casos especiales que requieren un tratamiento diferente:
Fracciones con numerador cero
Una fracción con numerador cero siempre es igual a cero, independientemente del denominador. Esto se debe a que cero no tiene ningún valor que añadir a la suma.Ejemplo:“`
/5 + 1/5 = 0
“`
Fracciones con denominador cero
Una fracción con denominador cero no está definida. Esto se debe a que dividir por cero no es posible en matemáticas. Por lo tanto, cualquier fracción con denominador cero se considera indefinida.Ejemplo:“`
/0 es indefinida
“`
Fracciones mixtas
Una fracción mixta es una combinación de un número entero y una fracción propia. Para sumar fracciones mixtas, primero debemos convertirlas en fracciones impropias y luego sumarlas.Ejemplo:“`
1/2 + 2 1/3
= 3/2 + 7/3= (9 + 14)/6= 23/6“`
Ejercicios y problemas
Los siguientes ejercicios y problemas están diseñados para ayudar a los niños de tercer grado a practicar la suma de fracciones.
Los ejercicios varían en dificultad, desde principiantes hasta avanzados. Se proporcionan las respuestas para todos los ejercicios.
Ejercicios para principiantes
- Suma las siguientes fracciones: 1/2 + 1/2
- Suma las siguientes fracciones: 1/4 + 1/4
- Suma las siguientes fracciones: 1/3 + 1/3
Ejercicios intermedios
- Suma las siguientes fracciones: 1/2 + 1/4
- Suma las siguientes fracciones: 1/3 + 1/6
- Suma las siguientes fracciones: 1/4 + 1/8
Ejercicios avanzados
- Suma las siguientes fracciones: 1/2 + 1/3
- Suma las siguientes fracciones: 1/3 + 1/5
- Suma las siguientes fracciones: 1/4 + 1/6 + 1/8
Respuestas
- Ejercicios para principiantes:
- 1/2 + 1/2 = 1
- 1/4 + 1/4 = 1/2
- 1/3 + 1/3 = 2/3
- Ejercicios intermedios:
- 1/2 + 1/4 = 3/4
- 1/3 + 1/6 = 1/2
- 1/4 + 1/8 = 3/8
- Ejercicios avanzados:
- 1/2 + 1/3 = 5/6
- 1/3 + 1/5 = 8/15
- 1/4 + 1/6 + 1/8 = 11/24
En conclusión, Suma De Fracciones Para Niños De Tercero De Primaria es un recurso invaluable que ayuda a los niños a desarrollar su comprensión de las fracciones y sus operaciones. Con su enfoque claro y práctico, este artículo equipa a los estudiantes con las habilidades y la confianza necesarias para abordar problemas de suma de fracciones con facilidad.
FAQ Corner
¿Qué es una fracción?
Una fracción representa una parte de un todo y se escribe como dos números separados por una barra diagonal. El número superior (numerador) indica la cantidad de partes que se toman, mientras que el número inferior (denominador) indica el total de partes en el todo.
¿Qué significa sumar fracciones?
Sumar fracciones significa combinar dos o más fracciones para obtener una fracción equivalente que represente el total de las partes.
¿Cómo se suman fracciones con el mismo denominador?
Para sumar fracciones con el mismo denominador, simplemente suma los numeradores y mantén el mismo denominador.
¿Cómo se suman fracciones con diferente denominador?
Para sumar fracciones con diferente denominador, primero encuentra el mínimo común múltiplo (mcm) de los denominadores. Luego, convierte cada fracción a una fracción equivalente con el mcm como denominador y finalmente suma los numeradores.
